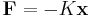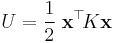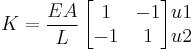Stiffness matrix

For the stiffness tensor in solid mechanics, see Hooke's law#Matrix representation (stiffness tensor).

In the finite element method and in analysis of spring systems, a stiffness matrix, K, is a symmetric positive-semidefinite matrix that generalizes the stiffness of Hooke's law to a matrix, describing the stiffness of between all of the degrees of freedom so that

\mathbf{F}=-K\mathbf{x}

where F and x are the force and the displacement vectors, and

U=\frac{1}{2} \;\mathbf{x}^\top\! K \mathbf{x}

is the system's total potential energy.

For a simple spring network, the stiffness matrix is a Laplacian matrix (in order to enforce Newton's third law) describing the connectivity graph between degrees of freedom. Off-diagonal entries contain 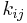k_{ij}, the negative stiffness of the spring connecting degree-of-freedom i to j. For example,

K=\left(\begin{array}{rrrrrr} 13 & -1 & 0 & 0 & -12 & 0\\ -1 & 3 & -1 & 0 & -1 & 0\\ 0 & -1 & 2 & -1 & 0 & 0\\ 0 & 0 & -1 & 3 & -1 & -1\\ -12 & -1 & 0 & -1 & 14 & 0\\ 0 & 0 & 0 & -1 & 0 & 1\\ \end{array}\right)

Contents

Truss Element Stiffness Matrix

The stiffness matrix of a horizontal prismatic truss element is [1] :


K = \frac{EA}{L} \begin{align} \begin{bmatrix} 1 & -1 \\ -1 & 1 \\ \end{bmatrix} \begin{matrix} u1 \\ u2 \\ \end{matrix} \end{align}

E: modules of elasticity

L: length

A: cross section area

Beam Element Stiffness Matrix

The stiffness matrix of a prismatic two dimensional horizontal beam element with negligible shear and axial deformation is[2] :

K = \frac{EI}{L} \begin{bmatrix} \frac{12}{L^2} & \frac{6}{L} & \frac{-12}{L^2}& \frac{6}{L}\\ \\ \frac{6}{L} & 4 & \frac{-6}{L} &2\\ \\ \frac{-12}{L^2}& \frac{-6}{L}&\frac{12}{L^2}& \frac{-6}{L}\\ \\ \frac{6}{L} & 2&\frac{-6}{L} &4 \end{bmatrix} :

The stiffness matrix of a prismatic two dimensional horizontal beam element with negligible shear deformation is[3] :

K = \begin{bmatrix} \frac{AE}{L} & 0 & 0& \frac{-AE}{L} & 0 & 0 \\ \\ 0 & \frac{12EI}{L^3} & \frac{6EI}{L^2} &0& \frac{-12EI}{L^3} &\frac{6EI}{L^2}\\ \\ 0 & \frac{6EI}{L^2} & \frac{4EI}{L} &0& \frac{-6EI}{L^2} &\frac{2EI}{L}\\ \\ \frac{-AE}{L} & 0 & 0& \frac{AE}{L} & 0 & 0 \\ \\ 0 & \frac{-12EI}{L^3} & \frac{-6EI}{L^2} &0& \frac{12EI}{L^3} &\frac{-6EI}{L^2}\\ \\ 0 & \frac{6EI}{L^2} & \frac{2EI}{L} &0& \frac{-6EI}{L^2} &\frac{4EI}{L}\\ \\ \end{bmatrix} :

E: modules of elasticity
I: section moment of inertia perpendicular to page
L: length

See also

References

  1. ^ McGuire, William; H.Gallagher, Richard; D.Ziemian, Ronald (2000). Matrix Structural Analysis. United States of America: John Wiley & Sons, Inc. pp. 16~18. ISBN 0-471-12918-6. http://www.amazon.com/Matrix-Structural-Analysis-William-McGuire/dp/book-citations/0471129186. 
  2. ^ D.Cook, Robert (1994). Finite Element Modeling for Stress Analysis. United States of America: John Wiley & Sons, Inc. pp. 20~22. ISBN 0-471-10774-3. http://www.amazon.com/Finite-Element-Modeling-Stress-Analysis/dp/0471107743. 
  3. ^ D.Cook, Robert (1994). Finite Element Modeling for Stress Analysis. United States of America: John Wiley & Sons, Inc. pp. 20~24. ISBN 0-471-10774-3. http://www.amazon.com/Finite-Element-Modeling-Stress-Analysis/dp/0471107743.